针对问题

找到一对无序的数中第  K  大，或者第 K 小的元素，返回该元素的值或者它的 index（index 的情况比较适合这堆数每个都独一无二的情况，不然可能会有多个答案）。

 

关键思想

拿一个数做参照，其他数通过对比它，来左右放置，得到的结果肯定是这个数在该数组中的排列位置是正确的。(DIvide and Conquer 分治思想)

 

形象讲解

把所有数字当成一个个球，假设我们要选出第 K 小的那个球。

 

我们有两个筐：A 和 B。

 

首先我们随机选择一个球作为参照物，然后我们开始分捡这一堆球：比它小的进入 A 筐，大于等于它的进入 B 筐。

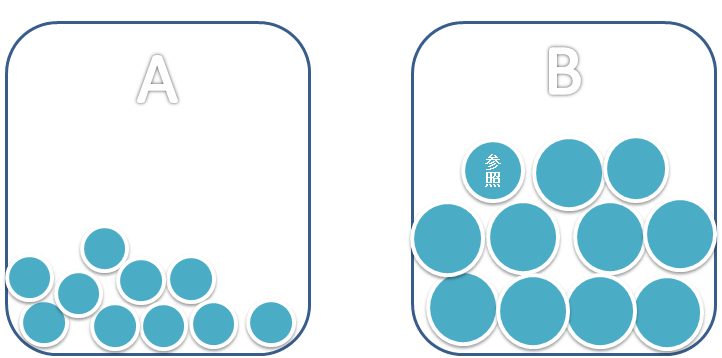
然后我们数一下 A 筐中有几个球。

如果刚好有 K-1 个，那么我们的参照物小球就是我们想要的那个第 K 个小球，不用忙活了，直接返回参照球；

如果小于 K-1 个，那么我们要的小球明显在 B 筐里面；我们排除掉 A 筐里面的 a 个球，则我们需要的是 B 筐中第 K-a 小的球，把筐清空，重新选择参照球，按上面流程再来一遍；

如果大于 K-1 个，那么我们要的小球明显在 A 筐里面；我们排除掉 B 筐里面的 b 个球，则我们需要的是 A 筐中第 K 小的球，把筐清空，重新选择参照球，按上面流程再来一遍。

 

实际与概念的区别

实际写代码的时候的操作，跟上面图解还是有些区别的。

上面的图解是为了简单粗暴快速将关键的概念融会贯通，而实际代码中，因为我们操作的是数组，而且为了防止递归迭代过程中无限循环，所以做了一些改进：

1. 不需要两个筐，在原数组上，选择最后一个元素作为参照数，浏览整个数组（除了参照数），然后在原数组上直接交换元素位置；

2. 直接操作数组的  start_index  和  end_index  就好，无需操作  k  ；

3. 递归迭代过程，与二分搜索的思路相似，为了防止出现递归下一层的数的数量与上一层相同，导致无限循环的情况，我们在下一层递归中，会将参照数拿走（即不会把参照小球放入 B 筐）。

 

JavaScript 代码

function quickSelect(nums, start, end, k){ //注意：k 是 zero-based 的，从零开始计数，而不是从一开始   if(start > end) return;    let pivot = nums[end];    let left = start;    for(let i=start; i
     
       或 <            [nums[i], nums[left]] = [nums[left], nums[i]];            left++;        }    }    [nums[left], nums[end]] = [nums[end], nums[left]];        if(left === k) return pivot;    if(left < k) return quickSelect(nums, left+1, end, k);    return quickSelect(nums, start, left-1, k);}
     

 

相关概念

pivot：轴，从无序数组中随机选取一个数字，或者取它的 first element 或 last element。

 

做题链接